Cálculo Integral: Clase#1 - 06/12/2021
Introducción al Cálculo Integral
Conceptos básicos:
Integración: Es un concepto fundamental de las matemáticas avanzadas.
Integral: Es una suma de infinitos sumandos, infinitamente pequeños.
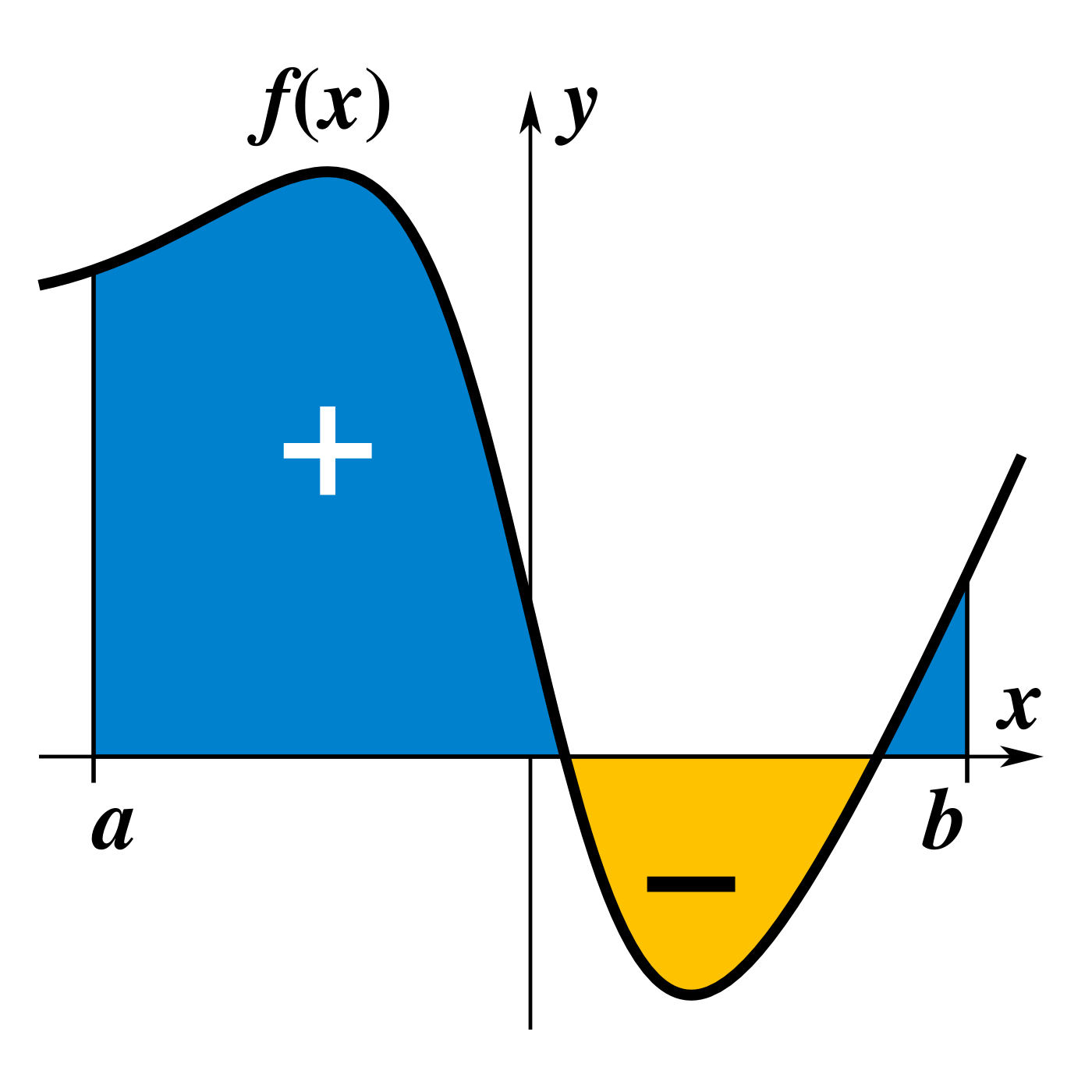
Integral definida: Representa el área limitada por la gráfica de la función.
Teorema Fundamental del Cálculo
El teorema fundamental del cálculo explica que la integración y la derivación son operaciones inversas.
En cálculo integral se emplean las diferenciales, de modo que a la derivada de una función se le agrega el factor dx.
La diferencial
La diferencial de una función es igual al producto de su derivada por la diferencial de la variable independiente
df (x) = f' (x)dx
Definición de integral definida
En cálculo integral se puede enunciar el problema:
- Dada la diferencial de una función, hallar la función.
- La operación la indicamos con el símbolo: ∫
- Por lo tanto se expresa: ∫ f' (x)dx = f (x)
La aplicación de las integrales definidas es muy común en la ingeniería y en la matemática en general. Se utiliza principalmente para el cálculo de áreas y volúmenes de regiones y sólidos de revolución.
Aplicaciones de los dx al cálculo de errores
